트리

• 사진 출처 : https://laurent.tistory.com/entry/자료구조-트리-Tree

• https://velog.io/@juwon9733/코딩-테스트를-위한-트리Tree-자료구조-10분-핵심-요약

• 강의 출처 : 동빈나

• 강의 출처 : 쉬운 코드

1. 트리

트리를 이용해 직접 구현하는 경우는 거의 없지만 관련 라이브러리나 문서를 이해할 때 좋다

🍇 트리란?

• 그래프 중 하나로 그래프의 특징처럼 정점과 간선으로 이루어져 있고, 트리 구조로 배열된 일종의 계층적 데이터의 집합

• 트리로 이루어진 집합을 숲이라고 함

• 뿌리가 최상위로 올라감

• 가계도와 같음 ⇒ 단군 할아버지가 A같은 느낌

🍇 트리의 특징

1. 부모, 자식 계층적 구조를 가진다.

2. 데이터를 순차적으로 저장하지 않는 비선형 구조

3. 트리에 서브트리가 있는 재귀적 구조

4. V-1 = E라는 특징을 가진다. 간선 수= 노드수 -1

5. 임의의 두 노드 사이 경로는 유일무이하게 존재한다.

6. 루트 노드는 하나만 존재한다.

7. 사이클(cycle)이 존재하지 않음

8. 자녀 노드는 하나의 부모 노드만 존재

🍇 트리의 용어

1. 루트 노드(Root Node)

   1. 트리에서 부모가 없는 최상위 노드, 트리의 시작점

   2. 2

2. 단말 노드(Termial Node) = 외부 노드(external) 노드

   1. 자식이 없는 노드, 트리의 가장 말단에 위치, degree가 0

   2. 3, 7, 8, 1, 4

   3. leaf node, outer node, terminal node

3. 레벨(Level)

   1. 노드와 루트 노드 경로에서 간선의 수

   2. 루트 노드의 레벨은 0 (or 1)

4. 조상 노드(Ancestor Node) : 부모 노드를 따라 루트 노트까지 올라가며 만나는 모든 노드

   1. 8의 조상 노드 : 11, 9, 2

5. 자손 노드(descendant Node) : 자녀 노드를 따라 내려가며 만날 수 있는 모든 노드

   1. 9의 자손 노드 : 11, 8, 1, 4

6. 자식 노드(Child Node) : 특정 노드에 연결된 다음 레벨의 노드

   1. 5번 노드의 자식 노드는 6, 7

   2. 6번 노드의 자식 노드는 3

7. 부모 노드(Parent Node) : 자녀 노드를 가지는 노드

   1. 2, 5, 9, 6, 11

8. 형제 노드(Sibling) : 같은 부모를 가진 노드

   1. {8, 1, 4}, {6, 7}, {5, 9}

9. 내부 노드(internal) =branch node = inner node : 자녀 노드를 가지는 노드

   1. 2, 5, 9, 6, 11

10. 노드의 깊이(Depth)

    1. 루트 노드에서 해당 노드에 도달하기 위한 간선의 수

    2. 11의 깊이 : 2

    3. 루트 노드의 깊이 : 0

11. 트리의 깊이(depth)

    1. 트리에 있는 노드들의 깊이 중 가장 긴 깊이

    2. 트리 깊이 : 3

    3. 트리 높이 = 트리 깊이

12. 경로(path)

    1. 한 노드에서 다른 노드 사이의 노드들의 시퀸스(sequence)

    2. 2에서 7로의 경로 : 2- 5 -7

    3. 경로 길이(length of path)

    4. 경로에 있는 노드들의 수

    5. 2에서 7로의 경로 길이 : 3

    6. 2에서 3으로의 경로 길이 : 4

13. 노드의 높이(height) : 문서마다 높이를 간선으로 따지기도 하고 노드 수로 따지기도

    1. 노드에서 리프(leaf) 노드까지의 가장 긴 경로의 간선(edge) 수

    2. 5의 높이 : 2

    3. 리프(left) 노드의 높이 : 0

14. 트리의 높이

    1. 루트 노드의 높이

    2. 트리 높이 : 3

15. 차수(Degree)

    1. 특정 노드의 연결된 자식 노드의 수

    2. 차수를 고르라는데 특정 노드 언급 x => 가장 큰 차수를 가지는 값을 고르면 됨 = 트리의 차수(degree)

    3. 11의 차수 : 3

    4. 3의 차수 : 0

16. 노드의 크기(size)

    1. 자신을 포함한 자손 노드의 수

    2. 9의 크기 : 5

    3. 5의 크기 : 4

17. 트리의 크기(size)

    1. 트리의 모든 노드의 수

    2. 트리의 크기 : 10

18. 두 노드 사이의 거리(distance)

    1. 두 노드의 최단 경로의 간선 수

    2. distance(9, 8) : 2

    3. distance(3, 8) : 6

19. width

• 임의의 레벨에서 노드의 수

• level 2의 width : 3

1. 서브 트리(subtree) : 각 노드의 자녀 노드들을 재귀적으로 서브 트리를 구성한다.

🍇 트리를 사용하는 곳[chat gpt]

계층 구조를 나타내거나 데이터를 조직화하여 사용되는 중요한 자료구조

2. 이진 트리

🍇 이진 트리(Binary Tree)

• 각 노드의 자녀 노드 수 최대 2개인 Tree를 의미

• left child | right child = 왼쪽 자녀 노드 | 오른쪽 자녀 노드

🍇 이진 트리(Binary Tree) 종류

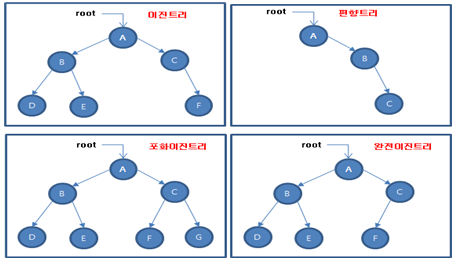
1. full binary tree(정 이진 트리) : 모든 노드는 자녀 노드가 없거나 두 개인 트리 = 자녀 노드가 1개인 노드는 없다.

1. complete binary tree(완전 이진 트리) : 마지막 레벨을 제외한 모든 레벨에서 노드가 빠짐없이 채워져 있고 마지막 레벨은 왼쪽부터 빠짐없이 노드가 채워져 있는 트리

1. perfect binary tree(포화 이진 트리) : 모든 레벨에서 노드가 빠짐없이 채워져 있는 트리

1. degenerate binary tree(변질 이진 트리) : 모든 부모 노드는 하나의 자녀 노드만을 가짐

• pathological binary tree라고도 불림

• left skewed binary tree : 모든 부모 노드는 왼쪽 자녀 노드만 가지는 트리

• right skewed binary tree : 모든 부모 노드는 오른쪽 자녀 노드만 가지는 트리

1. balanced binary tree(균형 이진 트리) : 모든 노드에서 왼쪽 서브 트리와 오른쪽 서브 트리의 높이 차이가 최대 1인 트리

1. 포화 이진 트리 : 모든 잎의 레벨이 동일한 이진 트리이며, 잎이 아닌 내부 노드들은 모두 2개의 자식을 가지는 트리

   • 내부 노드 : 루트 노드와 리프 노드(leaf node)를 제외한 나머지 노드를 의미

   • 잎 : 자식이 없는 노드

🍇 이진 트리 장점

1. 삽입 삭제가 유연하다

2. 값의 크기에 따라 좌우 서브트리가 나눠지기 때문에 삽입/삭제/검색이 보통은 빠르다

3. 값의 순서대로 순회가능

🍇 이진 트리 단점

• 최악의 경우 모든 트리에 있는 노드를 방문 해줘야 함

• 트리가 구조적으로 한쪽으로 편향되면 삽입, 삭제, 검색 등등 여러 동작들의 수행시간 악화

• 이 문제를 해결하기 위해 스스로 균형을 잡는 이진 탐색 트리가 사용

  • AVL 트리. Red-Black 트리

🍇 관련 코테 문제

예제 : 길찾기 문제

1. 문제 링크 : https://school.programmers.co.kr/learn/courses/30/lessons/42892

2. 다른 사람 풀이 : https://choichumji.tistory.com/167

3. 강사님의 코드와 설명 덧붙힘

   1. preorder.stream().mapToInt(Integer::intValue).toArray()

   2. preorder 리스트를 스트림으로 변환하고, 각 요소를 mapToInt() 메서드를 이용해 int 형으로 변환

   3. **mapToInt(Integer::intValue)**는 각 요소를 int로 변환하는 메서드 참

   4. **Integer::intValue**는 Integer 클래스의 intValue 메서드를 호출하여 int로 변환하는 것을 의미

   5. toArray() 메서드를 사용하여 해당 스트림의 요소들을 배열로 변환

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Solution {
    //이진 트리 노드(value : 노드 숫자 x,y : 노드 위치 - 좌표 )
    // left, right : 각각 왼쪽 자식인지 오른쪽 자식인지 구분
    private static class Node{
        public final int value;
        public final int x;
        public final int y;

        public Node left;
        public Node right;

        private Node(int value, int x, int y){
            this.value = value;
            this.x = x;
            this.y = y;
        }
    }

    // 노드를 삽입하는 메서드, 주어진 노드를 현재 노드의 왼쪽 또는 오른쪽에 삽입
    // 위치 좌표를 기준으로 비교하여 적절한 위치에 노드를 삽입
    private void insert(Node root, Node node){
        if(node.x < root.x) {
            if (root.left == null) {
                root.left = node;
            } else {
                insert(root.left, node);
            }
        }
        else{
            if(root.right == null){
                root.right = node;
            }
            else{
                insert(root, node);
            }
        }
    }

    //노드 배열을 받아 이진 트리를 생성하는 메서드
    // 배열의 첫 번째 노드를 루트로 지정하고, 나머지 노드들을 insert 메서드를 통해 적절한 위치에 삽입하여 전체 트리를 구성
    private Node constructTree(Node[] nodes){
        Node root = nodes[0];
        for(int i = 1; i<nodes.length; i++){
            insert(root, nodes[i]);
        }

        return root;}

    // 전위 순회
    // 노드를 방문하면서 노드의 값을 리스트에 추가한 후, 왼쪽 자식 노드를 재귀적으로 순회하고 오른쪽 자식 노드를 재귀적으로 순회
    private void pre(Node node, List<Integer> visits){
        if(node == null) return;
        visits.add(node.value);  // 현재 노드 값을 방문 리스트에 추가
        pre(node.left, visits); // 왼쪽 자식 노드를 전위 순회
        pre(node.right, visits); // 오른쪽 자식 노드를 전위 순회
    }

    // 후위 순회
    // 노드의 왼쪽 자식 노드와 오른쪽 자식 노드를 재귀적으로 순회한 후, 현재 노드의 값을 리스트에 추가
    private void post(Node node, List<Integer> visits){
        if(node == null) return;
        // 끝부터 후
        post(node.left, visits);
        post(node.right, visits);
        // 마지막에 넣어줌
        visits.add(node.value);
    }

    public int[][] solution(int[][] nodeinfo)
    {
        Node[] nodes = new Node[nodeinfo.length];
        for (int i = 0; i < nodes.length; i++)
        {
            // 각 인덱스에 노드 정보 저장, i + 1은 노드의 값을 의미하며, nodeinfo[i][0]은 x 좌표, nodeinfo[i][1]은 y 좌표를 나타낸다
            nodes[i] = new Node(i + 1, nodeinfo[i][0], nodeinfo[i][1]);
        }

        Arrays.sort(nodes, (a, b) -> b.y - a.y); // 윗부분부터 순회하기 위해서 y좌표를 내림차순으로 정렬
        // 노드 정보들이 정렬되었으므로, 배열의 첫 노드부터 순회하며 트리를 구성한다.

        Node root = constructTree(nodes); // 이진 트리 생성

        List<Integer> preorder = new ArrayList<>();
        pre(root,preorder);

        List<Integer> postorder = new ArrayList<>();
        post(root,preorder);

        //  preorder와 postorder 리스트의 요소들을 각각 int 배열로 변환하여 최종적인 결과를 반환
        return new int[][] {
                preorder.stream().mapToInt(Integer::intValue).toArray(),
                postorder.stream().mapToInt(Integer::intValue).toArray(),
        };

    }
}

3. 이진 탐색 트리

🍇 이진 탐색 트리(Binary Search Tree)

• 이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조의 일종

• 이진 탐색 트리의 특징 : 왼쪽 자식 노드 < 부모 노드 < 오쪽 자식 노드

  • 부모 노드보다 왼쪽 노드가 작다.

  • 부모 노드보다 오른쪽 노드가 크다

  • 즉, 모든 노드의 왼쪽 서브 트리는 해당 노드의 값보다 작은 값들만 가지고 모든 노드의 오른쪽 서브 트리는 해당 노드의 값보다 큰 값들만 가진다.

• 탐색 범위가 이상적인 경우 절반 가까이 줄어든다.

• 하지만 반대로 균형이 맞지 않으면 검색 효율이 좋지 않다.

이진 탐색 트리의 최솟값과 최대값

• 최솟값 : 트리의 가장 왼쪽에 존재

• 최댓값 : 트리의 가장 오른쪽에 존재

🍇 트리 순회(Tree Traversal)

• 트리 자료구조에 포함된 노드를 특정한 방법으로 한 번 씩 방문하는 방법을 의미

  • 트리의 정보를 시각적으로 확인 가능

대표적인 트리 순회

1. 전위 순회(Pre-Order Traversal)

• Root ⇒ Left ⇒ Right 순으로 방문

• 루트를 먼저 방문

// 전위 순회
    private void pre(Node node, List<Integer> visits){
        if(node == null) return;
        visits.add(node.value);
        pre(node.left, visits);
        pre(node.right, visits);
    }

1. 중위 순회(In-Order traversal)

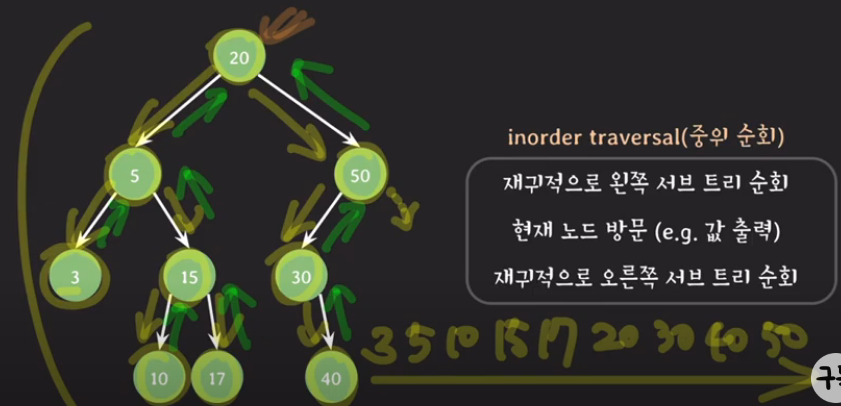
⇒ 작은값 기준으로 순서대로 방문

재귀적으로 왼쪽 서브 트리 순회 ⇒ 현재 노드 방문(값 출력) ⇒ 재귀적으로 오른쪽 서브 트리 순회

• left ⇒ Root ⇒ Right 순으로 방문

• 재귀적으로 왼쪽 자식을 먼저 방문 후 루트를 방문

1. 후위 순회(Post-Order)

• left ⇒ right ⇒ root 순으로 방문

• 오른쪽 자식을 방문 후 루트 방문

// 후위 순회
    private void post(Node node, List<Integer> visits){
        if(node == null) return;
        // 끝부터 후
        post(node.left, visits);
        post(node.right, visits);
        // 마지막에 넣어줌
        visits.add(node.value);
    }

비교

🍇 노드의 successor(후임자)

• 해당 노드보다 값이 큰 노드들 중에서 가장 값이 작은 노드

• 20의 successor : 30

• 17의 sucessor : 20

• 10의 sucessor : 15

🍇 노드의 predecessor(선임자)

• 해당 노드보다 값이 작은 노드들 중에서 가장 값이 큰 노드

• 20의 predecessor : 17

• 10의 predecessor : 5

• 40의 predecessor : 30

🍇 데이터를 넣는 과정

1. 루트 노드 : 50

2. 만약 70을 넣는다고 하면 루트 노드보다 크기 때문에 오른쪽에 집어 넣음

1. 만약 90을 넣으면 70보다 크기 때문에 오른쪽에 집어넣음

1. 99을 넣으면 50이랑 비교 후 크니까 오른쪽 ⇒ 70이랑 비교 후 크니까 오른쪽 ⇒ 90이랑 비교 후 크니까 오른쪽에 넣음 99

1. 80을 삽입하면 1) 50보다 크니까 오른쪽 2) 70보다 크니까 오른쪽 3) 90보다 작으니까 왼쪽에 최종 삽입

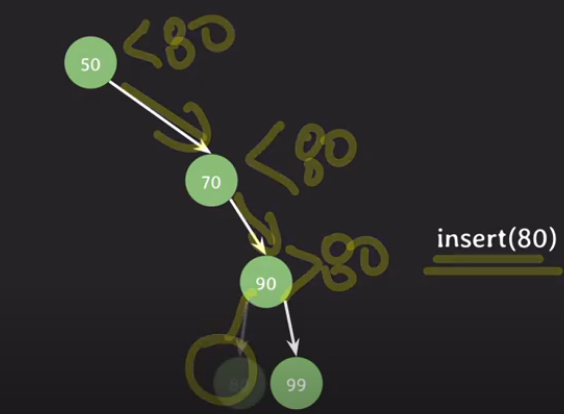
1. 이런 과정을 반복 ⇒ 최종 이진 트리

🍇 이진트리 삭제(delete)

과정

1. 삭제하려는 노드가 있는지 검색

2. 있으면 삭제

3. 20을 삭제하려면 1) 50보다 작으니 왼쪽 ⇒ 2) 30보다 작으니 왼쪽 ⇒ 20 발견 ⇒ 삭제 후 값이 null이 됨

1. 30을 지우려함 ⇒ 근데 자녀인 40이 있음

   1. 즉, 30의 부모인 50이 40을 가르키게 바꿈

1. 50을 지우려고 함 ⇒ 근데 자녀가 둘

   1. 둘 중 하나의 서브트리에서 오른쪽은 가장 작은 값을 위로 올림

   2. 왼쪽의 경우에는 가장 큰 값을 위로 올림

자녀가 없는 노드 삭제(delete)

• 삭제될 노드를 가리키던 레퍼런스를 가리키는 것이 없도록 처리 ⇒ null

자녀가 하나인 노드 삭제(delete)

• 삭제될 노드를 가리키던 레퍼런스를 삭제될 노드의 자녀를 가르키게 변경

자녀가 둘인 노드 삭제(delete)

• 삭제될 노드의 오른쪽 서브트리에서 제일 값이 작은 노드가 삭제될 노드 대체

🍇 데이터 추가

1. 현재 트리의 상태

1. 삽입이랑 비슷함 비교해서 넣기

1. 여기서 또 루트 노드 삭제되면

   1. 오른쪽에서 1) 가장 작은 값인 80이 위로 올라가고 2) 80의 자녀인 85는 80의 부모였던 90이 가르키게 됨

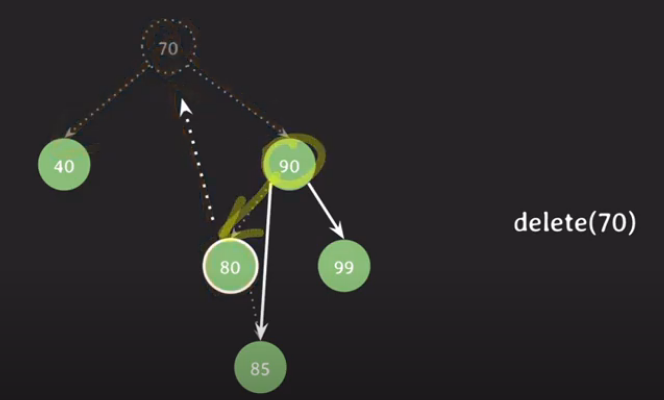
🍇 데이터를 조회하는 과정

이진 탐색 트리가 이미 구성되어 있다고 가정, 찾고자 하는 원소 : 37

1. 루트 노드부터 방문하여 탐색을 진행

   1. 현재 노드와 찾는 원소 37을 비교

   2. 찾는 원소가 더 크므로 오른쪽 방문

1. 현재 노드와 값을 비교

   1. 현재 노드와 찾는 원소 37을 비교

   2. 찾는 원소가 더 작으므로 왼쪽 방문

1. 현재 노드와 값을 비교

   1. 현재 노드와 찾는 원소 37을 비교

   2. 원소를 찾았으므로 탐색을 종료

4. AVL 트리

출처 : http://yahma.tistory.com/85

🍇 정의

• 최악의 경우 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색 트리

• 두 자식 서브트리의 높이는 항상 최대 1만큼 차이 난다는 특징

• 탐색, 삽입, 삭제 모두 시간 복잡도가 O(logn)

🍇 균형 인수

1. 균형 인수 : 균형의 정도를 표현하는 단위

2. 균형 인수의 절댓값이 크면 클수록 그만큼 트리의 균형이 무너진 상태

3. 균형 인수 값 = 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이

4. AVL 트리는 두 자식의 서브트리의 높이가 항상 최대 1만큼 차이 나기 때문에 절댓값이 2이상인 경우 위치 재조정 진행

🍇 균형잡는 과정

1. LL 상태 : 균형인수 + 2가 존재하는 상태

2. LL 회전 : LL상태의 데이터를 균형 잡기 위해 회전하는 방법

3. RR 상태 : 균형 인수 -2가 존재하는 상태

4. RR 회전 : RR 상태의 데이터를 균형잡기 위해 회전하는 방법

레드 블랙 트리

• 모든 리프 노트와 루트 노트는 블랙이고 어떤 노드가 레드이면 그 노드의 자식은 반드시 블랙이다.