Big O

1. 자료구조와 알고리즘이 필요한 이유

1) 프로그래밍 언어란?

컴퓨터 프로그래밍에서 어떠한 알고리즘을 구현하기 위해서 쓰여지는 언어

자료구조와 알고리즘에 대한 이해가 있다면 구현하고자 하는 기능을 보다 쉽고 효울적으로 만들 수 있게 도와줌

현업의 경우 코딩테스트를 공부하지 않음 대부분은 언어나 프레임워크나 라이브러리에서 이미 잘 만들어진 아이들을 가져와서 만들고자 하는 기능을 가져와서 사용

2) 그렇다면 왜 코딩테스트를 볼까?

알고리즘 작성 후 질의/응답을 통해 자료구조와 알고리즘에 대해 얼마나 이해하고 있고 시간과 공간 복잡도에 대한 이해가 있는지 확인해보기 위함

EX.

• 하필 이 알고리즘을 선택한 이유는?

• 이것이 저것들의 비해 장단점은?

• 저것과 이것의 차이는?

2. 알고리즘과 자료구조를 공부방법

자료 구조는 어느 상황에 쓰이는 것이 좋고 또 어떤 식의 API들이 있는지 이런 것들 조금 큰 그림을 보면서 공부

1) 자료구조

서비스나 어플리케이션에 필요한 데이터를 메모리에 어떻게 구조적으로 잘 정리해서 담아두고, 관리하고 효율적인 방식으로 필요한 데이터에 빠르게 접근하고 필요한 수정 삽입 삭제 할 수 있도록 도와준다. 기능에 적합한 알맞는 자료구조를 쓰는 것이 중요하다.

💡 자료 구조 공부시 Point

1. Order : 자료 구조 안에 있는 데이터들의 순서가 보장?

2. Unique : 중복된 데이터가 들어 갈 수 있는가?

3. Search : 검색에 얼마나 효율적인가?

4. Modification : 우리가 원하는 기능에 따라서 수정시 얼마나 효율적인지?

3. BigO

출처 : 니꼴라스 https://www.youtube.com/watch?v=BEVnxbxBqi8

1) 개요

• 알고리즘의 스피드를 어떻게 표현하는지 알아봄

• 빠르다, 느리다의 말이 아닌 CS지식

2) 알고리즘

---

제한된 공간과 시간 안에서 데이터를 어떻게 처리할 것인지를 정해놓은 로직

주어진 데이터를 검색하거나 정렬 또는 총점을 구하는 등의 다양한 계산을 할 수 있는 것을 말함

즉, 주어진 input으로 정의된 계산을 수행한 다음 output 결과값을 내는 것

3) 시간복잡도

---

💫 문제를 해결하는 데 걸리는 시간과 입력의 함수 관계

1. “빠르다”, “느리다”는 시간으로 표현하지 않음(시간 복잡도)

   • 같은 알고리즘이라도 내 컴퓨터가 친구의 컴퓨터보다 빠를 수 있음

   • 컴퓨터라는 하드웨어가 결정하기 때문

   • “완료까지 걸리는 절차의 수”STEPS

   • 알고리즘을 위해 필요한 연산의 횟수

   • 특정 크기의 입력에 대하여 알고리즘이 얼마나 오래 걸리는지

2. 선형 알고리즘의 경우 사이즈가 N개이면, N스텝이 필요함

4) 공간복잡도

---

• 공간복잡도 : 특정한 크기의 입력에 대하여 알고리즘이 얼마나 많은 메모리를 차지하는지

• 알고리즘을 위해 필요한 메모리의 양

• 예를 들어 int a[1004];라는 배열이면 a 배열은 1004X4바이트의 크기를 가지게 됨

5) Big O

---

💫 사이즈가 N개면, N스텝이 필요해요!!! 보다는 선형검색의 시간 복잡도 = O(N) 이렇게 설명하는 컨셉을 Big O

1. Big O란 시간복잡도를 표현하는 표기법

2. 언제 무엇을 쓸지 빠르게 파악 가능하며, 자신의 코드를 평가 가능

   • 왜..? 미래에 어떻게 작동할 수 있는지 알 수 있으니

   • Big O를 이해시, 알고리즘을 빠르게 분석 가능, 언제 무엇을 쓸지 파악 가능

3. 알고리즘의 퍼포먼스를 이해하기 쉽고 효율적으로 작성하는 방법

• 선형검색의 시간 복잡도 = O(N)

• but, 항상 Big O가 모든 알고리즘을 완벽히 설명하는 것은 아님

1. 배열을 인풋으로 사용할 함수, 인풋의 크기 상관없이 동일한 수의 스텝이 필요

   • 아래의 코드는 print_first라는 파이썬 함수를 정의하며, 매개변수 arr에게 받으며, arr의 첫 번째 인덱스를 출력해냄

   • 인덱스를 이용하여 한 번에 찾으니까

   • 이 함수의 시간복잡도는 constant time(상수 시간) : N의 크기 상관없이 끝내는데 동일한 숫자의 스텝이 필요

def print_first(arr):
		print(arr[0])

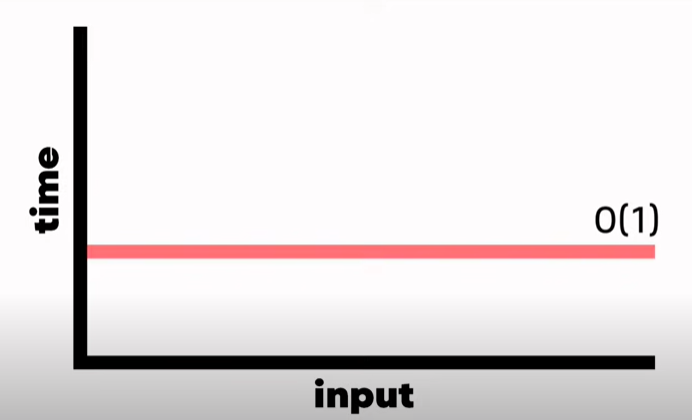
1. 이 코드의 경우 2번의 print가 있는데 2개의 스텝이 필요한 것

def print_first(arr):
		print(arr[0])
		print(arr[0])

💫 이렇다면 O[2] 일까? NO! 여전히 O[1]

• Big O는 함수의 디테일에 관심이 없고, 러프하게 어떻게 이 함수가 인풋의 사이즈에 따라서 어떻게 작동하는지가 중요

• 함수는 인풋 사이즈가 엄청나게 커져도 상관없이 미리 정해진 숫자에 따라 작동

1. 즉, Big O는 큰 원리에만 관심을 가짐

2. 꼭 기억해 둬야 할 것은 빅오는 상수를 신경 쓰지 않음

6) Constant Time Algorithm(상수 시간 알고리즘)

---

• constant time (일정한 시간/상수)

• 인풋사이즈와 관계없이 스텝이 정해진 알고리즘들

• 항상 선호하는 것 ⇒ 인풋이 늘어나도 변하지 않음

• 현실적으로 항상 만들기 힘들다

O(n) 자바 코드로 나타내면

// 시간 복잡도 O(n)이 계산된다. O(1)
public class OneToSum {

    public int sum(int n){
        int sum = 0;

        return n * (n + 1) / 2;
    }


    public static void main(String[] args) {
       int n = 5;
       // static으로 주지 않을 때
       OneToSum object = new OneToSum();
       System.out.println(object.sum(10));
    }
}

7) 시간복잡도 1: Big O의 시간복잡도, 선형 시간 복잡도

---

배열의 사이즈가 10이라면, 10번 프린트 하는 함수 : O(N)

def print_all(arr):
	for n in arr:
		print(n)

Q: 만약 반복문을 두번이라면 O(2N)일까? ****

def print_all(arr):
	for n in arr:
		print(n)
	for n in arr:
		print(n)

A: 2는 상수이기에 버려두고, 여전히 O(N)으로 표현, 핵심은 변하지 않았지 때문

메세지가 같다 ⇒ 인풋이 증가하면 스텝도 선형적으로 증가

O(N)이나 선형 시간복잡도를 그래프

8) 시간복잡도 2 : Quadratic Time(2차 시간)

---

• Nested Loops(중첩 반복)이 있을 때, 발생

• 아래의 경우 배열의 각 아이템에 대해 루프를 반복, 실행

def print_twice(arr)
	for n in arr:
		for x in arr:
			print(x, n)

• 시간복잡도 : 인풋 $n^2$

  EX. 인풋이 10개시 100번의 스텝 : 루프 안의 루프에서 함수를 실행시키기 때문

2차 시간복잡도 그래프를 선형 시간복잡도와 비교 그래프

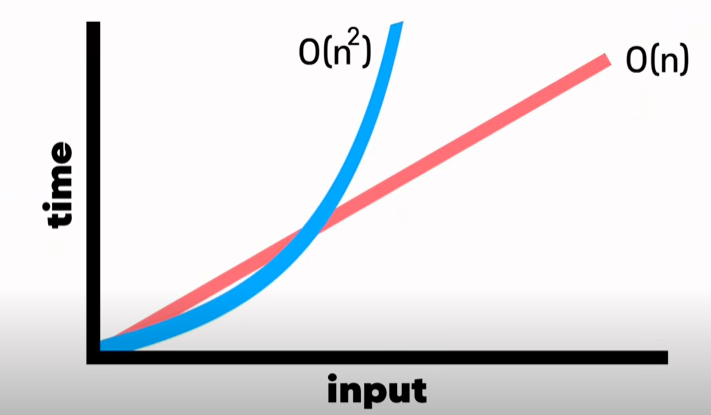
선형 시간복잡도가 2차 시간복잡도보다 더 효율적

9) 시간복잡도 3 : 로그 시간(Logarithmic Time)

---

1. 이진검색 알고리즘 설명시 사용 ⇒ 얼마나 빠른지 설명 가능

   1. 이진 검색 알고리즘은 인풋 사이즈가 2배가 되어도 필요한 step의 수는 1개밖에 안들어남

   2. 왜냐? 이진검색은 각 프로세스의 스텝을 절반으로 나눠서 하기 때문이

2. 표현법 : O(log N)

3. 정렬된 배열에만 사용 가능

4. exponent(지수) ↔ logarithm(로그)

• n = $log_232$ n은 32를 2로 몇번을 나눠야 1이 나올까?

💫 32 / 2 = 16 ← 1 16 / 2 = 8 ← 2 8 / 2 = 4 ← 3 4 / 2 = 2 ← 4 2 / 2 = 1 ← 5 times

• n은 5

  ⇒ 이진 검색과 같음 인풋을 반으로 나누고 시작하는 것처럼

  ⇒ Big O의 특성상 n = $log32$ 아래의 2가 사라짐

  ⇒ So, log N이 되는 것

• 로그 시간복잡도의 그래프

선형시간보다는 빠르고, 상수 시간보다는 느림

10) O(1) & O(N) & O(logN) 그래프

---

O(1) > O(logN) > O(N) 순으로 가장 효율적이다.

O(logN)은 아주 조금씩 증가하는 곡선을 그리고 있는데 O(1)보다는 덜 효율적이지만 O(N)보다는 훨씬 효율적이다.

사진 출처 : https://velog.io/@welloff_jj/Complexity-and-Big-O-notation

11) 그렇다면 연습문제

---

출처 : https://velog.io/@on-n-on-turtle/누구나-자료구조와-알고리즘-빅오표기법

📖 리스트 내 모든 항목을 출력함

public static void printThings() {
    String[] things = {"apples", "chairs", "files", "notes"};

    for (String thing : things)
        System.out.printf("Here's a thing : %s \n", thing);
}

이 알고리즘의 for루프에서 배열의 원소가 4개이기 때문에 4단계가 걸린다.

만약 배열의 원소가 10개이면 10단계가 걸릴 것이다.

for루프에 대입되는 배열의 원소 갯수만큼 단계가 걸리므로 이 알고리즘의 효율성은 O(N)이다.

📖 주어진 해가 윤년인지 알아봄

public static boolean isLeapYear(int year) {
    return (year % 100 == 0) ? (year % 400 == 0) : (year % 4 == 0);
}

N은 number이다.

함수로 전달된 수에 상관없이 단계 수가 일정하므로 O(1)알고리즘이다.

12) 스터디에서 얻은 자주 쓰이는 자료구조의 시간복잡도 정리

8월 23일 국비 강의 들으면서 저번주에 진행한 스터디에서 다른 분이 정리 한 추가 내용

1️⃣ 배열

1. 삽입/삭제: O(N)

2. 탐색: O(1)

👉 파이썬에서는 단순히 List로 구현한다. 👉 탐색할 때 사용하기 좋은 자료구조(삽입이나 삭제는 한자리씩 뒤로 옮기거나 하는 식으로 이루어질 수 있기 때문에, 시간복잡도가 O(N)이된다.)

2️⃣ 벡터 (= 동적배열)

삽입/삭제: O(N)

탐색: O(1)

👉 파이썬에서는 단순히 List로 구현한다. C++ 같은 언어에서는 배열과 벡터는 다르다. 하지만 파이썬에서는 배열과 같은 List로 쓰면 된다. List 자체가 이미 동적 배열을 지원해주기 때문이다.

3️⃣ 연결리스트

1. 삽입/삭제: O(1)

2. 탐색: O(N)

1. 링크드 리스트

👉 시간복잡도 측면에서 배열(List)와 반대 된다. (탐색을 하려면 순간적으로 포인터 부분을 찍고 찍고 가야 하기 때문에 탐색이 O(N)이 되고, 연결 자체의 앞뒤로 수정만 하면 되므로 삽입/삭제시 시간 복잡도가 O(1)이 된다.

👉 링크드 리스트는 백준 문제를 풀며 막 사용할일이 많지는 않지만, 다른 자료구조 구현에도 많이 쓰이니 이론상 알아둘 필요가 있다.

(면접질문으로도 나올 수 있겠다! ex) "우리 프로그램은 삽입/삭제가 빈번한데 어떤 자료구조를 쓸텐가??")

4️⃣ 스택 LIFO

1. 삽입/삭제: O(1)

👉 Last In First Out 👉 파이썬에서 구현은 List로 한다.

s = [1,2,3,4,5,6]

while(len(s)>0):
	print(s[-1])
    s.pop(-1)

위의 코드 처럼 구현 되면 되는데, 배열의 마지막 거를 꺼내는 거다.

5️⃣ 큐 LILO

1. 삽입/삭제: O(1)

👉 줄서기 Last in Last Out 👉 from collections import deque 로 임포트하여 데큐를 사용한다.

from collectionsimport deque

q = deque()
q.append(1)
q.append(2)
q.append(3)

while(len(q) >0):
	print(q.popleft())

위 코드에서 보면 popleft() 라는 함수를 통해 처음에 있는 값을 빼는데, 데큐는 popright()라는 함수도 지원한다.

👉 또한 파이썬에는 Queue도 있고 Deque도 있는데 Queue는 멀티 스레딩도 지원하는 라이브러리여서 Deque보다 느리다. 알고리즘 문제를 푸는 입장이므로 Deque를 사용하는 것이다.

6️⃣ 우선순위큐(내부가 Heap으로 구성)

1. 삽입/삭제 : O(logN)

import heapq

# 리스트를 하나 만들고 사용한다.
pq = []
heapq.heappush(pq,3)
heapq.heappush(pq,1)
heapq.heappush(pq,2)

while(len(pq) >0):
	print(heapq.heappop(pq))

👉 파이썬은 MinHeap 이다.(이진트리의 최상위는 항상 최소값인)

👉 우선 순위 큐 같은 경우에는 , 문제를 풀면서 여러 값들을 넣고 뺄때마다 젤 작은 값이나 젤 큰 값을 알아야 할 때 써야 한다. Sort() 같은 경우 전체 리스트 자체를 정렬해준다는 점에서 큰 차이점을 가진다.

7️⃣ Map(딕셔너리)

1. 삽입/삭제: O(1)

👉 파이썬은 딕셔너리를 사용하면 된다.

추가로, c++같은 경우는 O(logN)이 되는데 이는 c++의 맵은 속을 들여다 보면 이진 그래프로 구현이 되어있기 때문이고, python의 딕셔너리의 경우는 해시로 구현이 되어있기 때문이다.

8️⃣ 집합(set)

삽입/삭제: O(logN)

👉중복을 제거하는게 큰 특징!

13) 빅오의 실행 시간이 짧은 것부터 오래 걸리는 것까지 나열

1. O(1) - 상수 시간(Constant Time): 입력 크기와 상관없이 항상 일정한 시간이 소요

2. O(log n) - 로그 시간(Logarithmic Time): 입력의 크기에 대해 로그의 형태로 증가하는 시간이 소요

3. O(n) - 선형 시간(Linear Time): 입력 크기에 비례하여 시간이 선형으로 증가

4. O(n log n) - 선형 로그 시간(Linearithmic Time): n과 log n의 곱만큼 시간이 증가

5. O(n^2) - 이차 시간(Quadratic Time): 입력 크기의 제곱에 비례하여 시간이 증가

6. O(n^k) - 다항 시간(Polynomial Time): 입력 크기의 k 제곱에 비례하는 시간이 소요(k는 상수).

7. O(2^n) - 지수 시간(Exponential Time): 입력 크기에 대해 지수적으로 시간이 증가

8. O(n!) - 팩토리얼 시간(Factorial Time): 입력 크기의 팩토리얼에 비례하는 시간이 소요